Düzlemlere Farklı Bir Bakış
Genellikle bir düzlem tanımlanırken iki doğrusal olmayan 3-boyutlu vektör alınır ve bunların vektörel çarpımı hesaplanır bu vektörel çarpımın sonucuna normal vektör ( \vec{N} ile gösterelim) denir, daha sonra ise düzlemin geçeceği bir nokta (A ile gösterelim) belirlenir, daha sonra ise düzlemde hayali bir nokta (X ile gösterelim) alınarak bu iki noktanın doğrultusundaki vektör \vec{AX}=\vec{V} ile düzlemin normal vektörü olan \vec{N} nin dik olacağı anlaşılarak \vec{N} \bullet \vec{V} iç çarpımı 0 a eşitlenerek bir düzlem denklemi elde edilir.
Bu yazıda bu \vec{N} vektörünü doğrudan hesaplamadan, düzlemleri nasıl ifade edebileceğimizi inceleyeceğiz.
Öncelikle bir düzlem ifade edeceksek bu düzlemin geçeceği bir noktayı önceden kabul etmek gerekir, kabul edelim ki bizim düzlemimiz A=(x_0,y_0,z_0) şeklinde bir noktadan geçiyor olsun. Şimdi bu düzlemin tanımlanabilmesi için iki vektöre ihtiyaç vardır, bu vektörlere üreteç vektörler diyeceğiz, üreteç vektörlerimiz:\vec{u}=(u_0,u_1,u_2) ve \vec{v}=(v_0,v_1,v_2) olsunlar, şimdi düzlemimizi tanımlamaya hazırız, düzlemimizi aşağıdaki kümeyle ifade edebiliriz:
Buradaki \vec{OA}+t.\vec{v}+r.\vec{u} ifadesi düzenlenebilir:\vec{OA}+t.\vec{v}+r.\vec{u}=(x_0,y_0,z_0)+t.(v_0,v_1,v_2)+r.(u_0,u_1,u_2)Vektör toplama da yapıldığında:\vec{OA}+t.\vec{v}+r.\vec{u}=(x_0+t.v_0+r.u_0,y_0+t.v_1+r.u_1,z_0+t.v_2+r.u_2)Ki bunun da \vec{OX} olduğunu kabul etmiştik, şimdi\vec{OX}=(x,y,z)=(x_0+t.v_0+r.u_0,y_0+t.v_1+r.u_1,z_0+t.v_2+r.u_2)Buradansa aranan noktalar kümesinin şu şekilde ifade edilebileceği görülür:
Bunu kısaca söz ile özetlersek, bir düzlem bir A noktasının doğrusal olmayan \vec{v} ve \vec{u} vektörleri ile tüm ötelenişlerinin bir kümesidir.
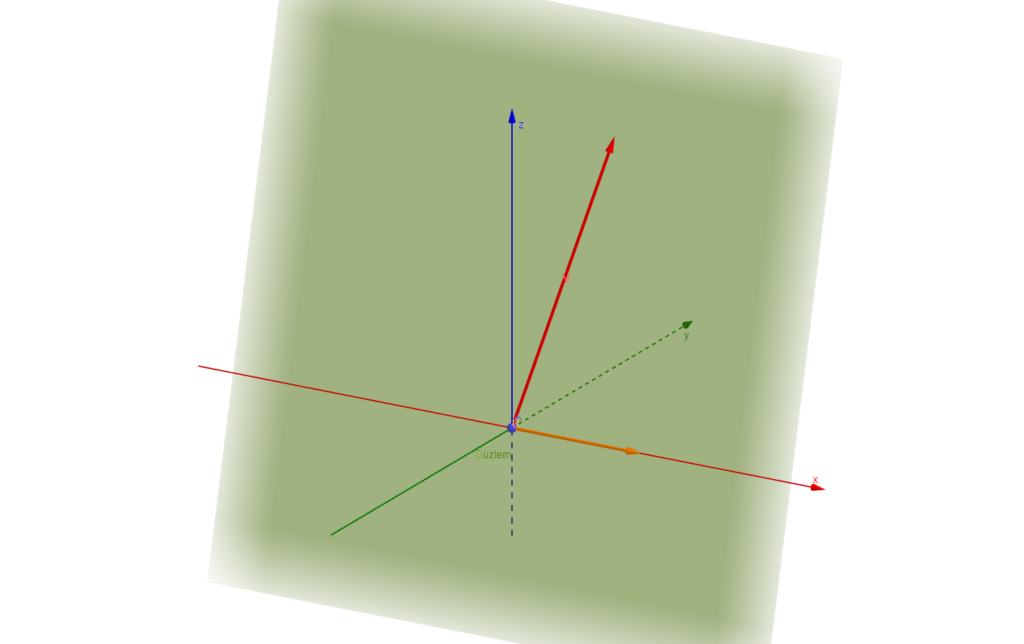
Vektörleri kırmızı ve turuncu renklerle gösterilmiş başlangıç noktası A olan yeşil renkli düzlem.